Manifold-Constrained Hyper-Connectionsとは
新年あけましておめでとうございます。PredNext代表の徳永です。今日は、お正月の間、X(Twitter)のおすすめタブにやけにたくさん出てきていた mHC: Manifold-Constrained Hyper-Connections を解説します。
HC (Hyper-Connections)
mHCの準備として、まずHyper-Connectionsについて解説します。Hyper-Connections の論文から画像を引用します。Hyper-Connectionsにはstatic Hyper-Connectionsとdynamic Hyper-Connectionsの2種類がありますが、図はstatic Hyper-Connectionsを表したものです。
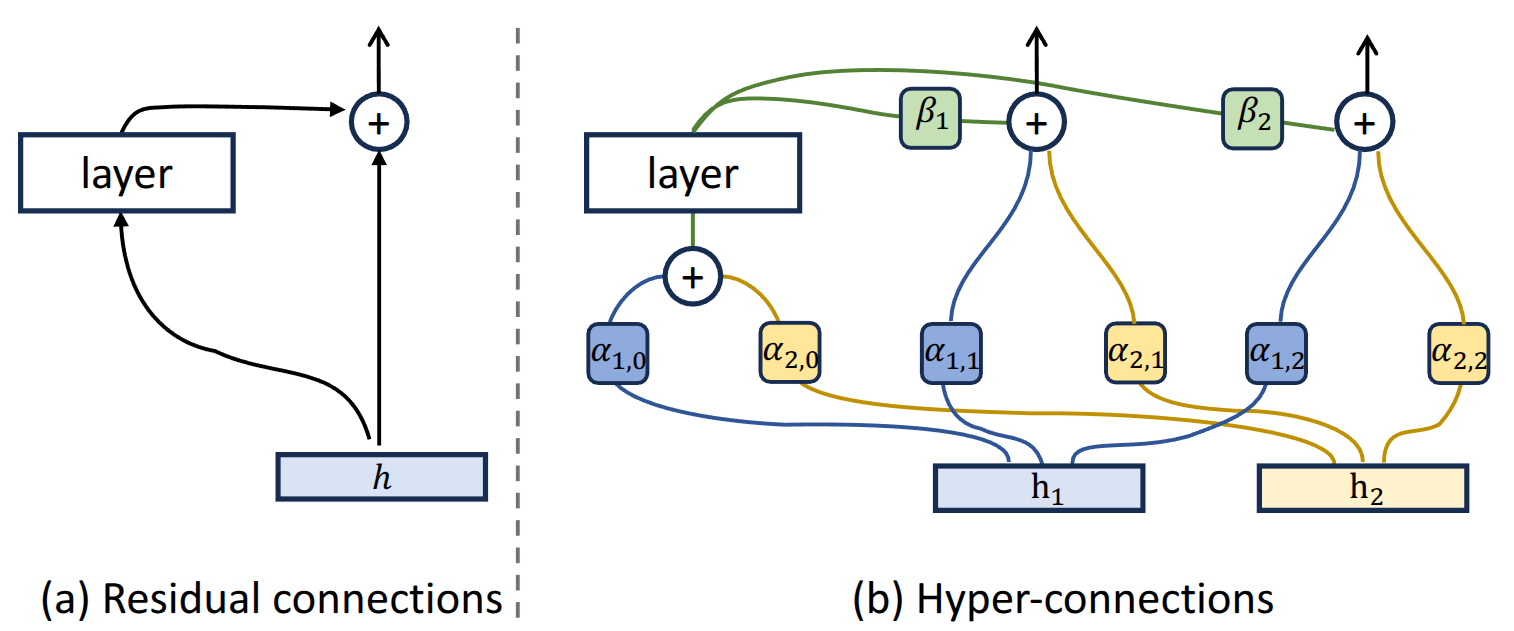
static Hyper-Connections
Transformer(図の左側)では、1トークンに対応するLLMの中間状態は通常は一本のベクトルですが、Hyper-Connections(図の右側)では複数のベクトルを用意します。上の図では、二本のベクトルを用意しています。この場合、HCは以下の3つの計算で構成されることになります。
- を MLP + Attentionに入力する
- を次のレイヤーに対するとする
- を次のレイヤーに対するとする
, は学習可能なscalar値です。添字がちょっとごちゃごちゃしてますが、図を見ればやりたいことは明瞭でしょう。ベクトルの本数を本とすると、で必要なパラメーター数は合計で個です。
dynamic Hyper-Connections
dynamic Hyper-Connectionsでは、先程の個のパラメーターを単純なscalar値として学習するのではなく、入力値から計算する(ためのパラメーターを学習する)ように変更します。
詳細な説明は省きますが、 という感じの雰囲気です。主な計算としては、入力ベクトルに対して変換行列を乗じて次元を落として、そこに更にを適用しています。
mHC (Manifold-Constrained Hyper-Connections)
mHCでは、HC(Hyper-Connections)の問題として、skip connectionがもはや単純なskip connectionではなく、scaling factor (HCではと表記されていた部分ですね)の値によってスケールが支配されてしまうこと、その の値域に制約がないために学習の安定性が損なわれてしまうことを指摘しています。
この問題を解決するため、mHCでは、HCで出てきた先程の個のscaling factorに対して制約をかけます。特に、に対しては、Sinkhorn-Knopp operatorを用いて制約をかけます。これは、行列の要素に対してまずを適用して値を全て正の領域に押しやり、その後、行単位と列単位で、各行、各列の和が1になるようにscalingを繰り返す操作です。無限に繰り返すと収束するそうなのですが、計算時間は有限なので、こちらの論文では20回程度で操作を打ち切っています。
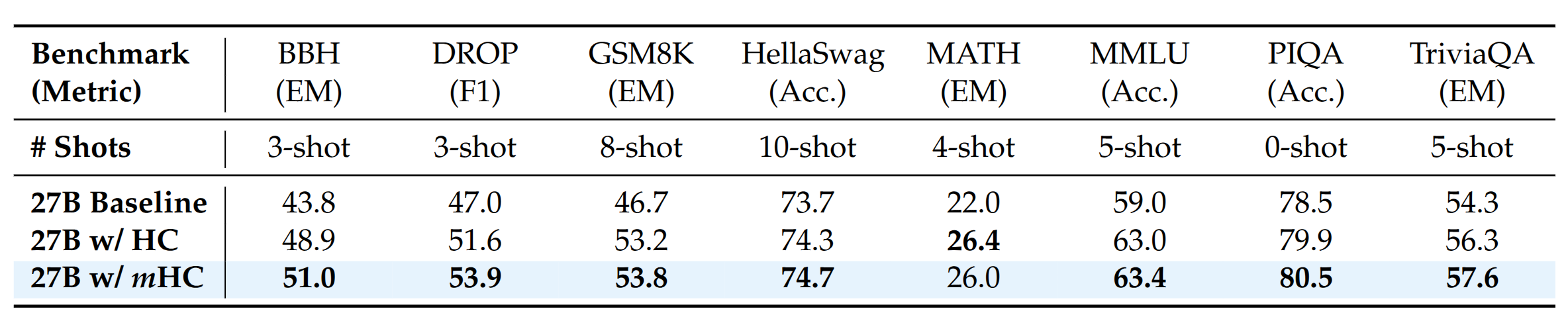
27Bモデルを用いた8つの実験では、mHCはbaselineと比較して、数pt程度の下流タスクの性能向上が得られました(下図はmHC: Manifold-Constrained Hyper-Connectionsより引用)。baselineからHCへの精度向上が大きく、mHCにすることで、そこからさらに1〜2pt程度の向上が得られています。
Transformerは主としてMLPとAttentionの2つの操作でじわじわと入力ベクトルを出力ベクトルへと変換していくモデルですが、HC/mHCは、パラメーター数、計算量ともにそれほど大きくなくとも有用な変換操作が存在しており、それをMLP/Attentionと補完的に用いることで性能向上が実現できることを示しています。追加パラメーターサイズはMLP等のレイヤーと比べるとほとんどないに等しく、記憶容量の向上にはほぼ寄与しないはずなので、記憶容量とは関係のない”かしこさ”(なんと表現すればいいのか、記憶容量みたいな便利な言葉が見つかりません)を向上させる変換操作がある、ということですね。
また、mHCでは実装上の工夫として、中間データが大量に増えるので、すべてのデータを残すのではなく、一部データはbackwardの際に再計算することで、HCと比較していくらかメモリ消費量を削減できた、という報告もありました。しかし、これは本質的にはmHC特有のメリットではなく、HCでも同様の工夫は可能であるように見えます。
所感
「記憶容量とは関係のない”かしこさ”(なんと表現すればいいのか、記憶容量みたいな便利な言葉が見つかりません)を向上させる変換操作がある」と書きましたが、このような変換操作はHC/mHCの他にもあるはずです。そう考えると、今のTransformerでは記憶、知識を取り出す操作と何かを考える操作が一つに癒着しており、不自然なように感じます。明示的に2つの操作を切り分けたネットワークをデザインできないものでしょうか。というのも、人間の脳と違って、計算機ではプロセッサとメモリの間の帯域が圧倒的なボトルネックになっているので、必要な分の知識だけを取り出して、それに対して出力を考えることができるようになれば、圧倒的に効率が良くなるはずです。MoEはそのような目的で作られていると思うのですが、さらにその「先」があるように感じます。
閑話休題、話を近い将来のLLMのアーキテクチャ改善に戻しましょう。Transformerの状態をベクトルではなく行列の形にするというと、どうしても、Parallel Scaling Law for Language Modelsを思い出してしまいます。これは、状態をベクトルから行列の形にしておくことで、MLPやAttentionの計算を行列積の形に持っていき、推論時にTensorCoreを活用できるようにします。これにより、実質的には計算量の増加をほぼ無視できる形で性能向上を実現する手法でした。HC/mHCとParallel Scaling Law、両方とも組み合わせて使うこともできそうです。
いずれの手法にせよ、推論時にkv cacheのサイズが増加してしまうことを防ぎようがない、というのが、泣きどころではあります。が、これは、これらの手法の問題というよりは、根本的に今のAttentionが抱える大きな問題であるというべきでしょう。そもそも、Attentionがなのがやりすぎなのであって、やっぱり、Attentionの計算量は くらいにおさえるべきだし、おさえられるはずだよなぁ、という思いを新たにしました。(は逆に減らしすぎだと感じるので、最近、状態空間モデルに対しては、個人的にはちょっと興味が下がっています。)
お仕事募集中
PredNextでは現在、2026年4月以降のお仕事の依頼をもう少しだけ募集しています。PredNextの得意分野は自然言語処理や画像処理を中心とするAI関連技術で、その中でもとくに軽量化、高速化を得意としています。ご興味を持たれた方はお問い合わせフォームからぜひお気軽にご連絡ください。