LLM #AI #LLM #量子化

1bit LLMの時代はいつ来るのか、それとも？

2025年6月20日

PredNext代表の徳永と申します。XなどではtkngというIDで活動しています。この10年ほどは公私ともにニューラルネットワークの軽量化に情熱を注いでおり、以前の職ではLeapMindという会社のCTOとして、極小量子化ニューラルネットワーク専用アクセラレーターや、fp8特化のニューラルネットワーク専用アクセラレーターの開発に携わっていました。

その縁で、1年ほど前に情報処理学会誌に「1bit LLM の時代は来るのか，来ないのか，どっちなんだい？」という記事を寄稿しました。内容はリンク先のWeb版で全文を無料でお読みいただけます。当時話題となっていたBitNet b1.58論文（正式名称：「The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits」、Microsoft研究チームによる研究）についての解説です。なお、「b1.58」という名前は、モデルのパラメーターを三値（-1, 0, 1）で表現するという意味です。3種類の値が均等にランダムに出現する場合、エントロピーが約1.58bitになることからb1.58と呼んでいるようです。

いきなり専門用語の羅列から始めてしまいましたが、そもそも量子化とはなんでしょうか？ 量子化とは、本来は連続値を離散値で近似することです。ただし、AI関連の分野では少し特殊で、32bit浮動小数点数を連続値とみなし、8bit以下にデータを離散化する操作を「量子化」と呼びます。例えば、通常の浮動小数点数は32ビットや16ビットで表現されますが、これを8ビット、4ビット、あるいは1ビットなどに減らすことで、モデルサイズを大幅に小さくできます。また、8bitよりも極端に小さなビット幅への量子化はextremely low bit quantizationやultra low bit quantizationと呼ばれ、これを日本語では「極小量子化」と呼んでいます。

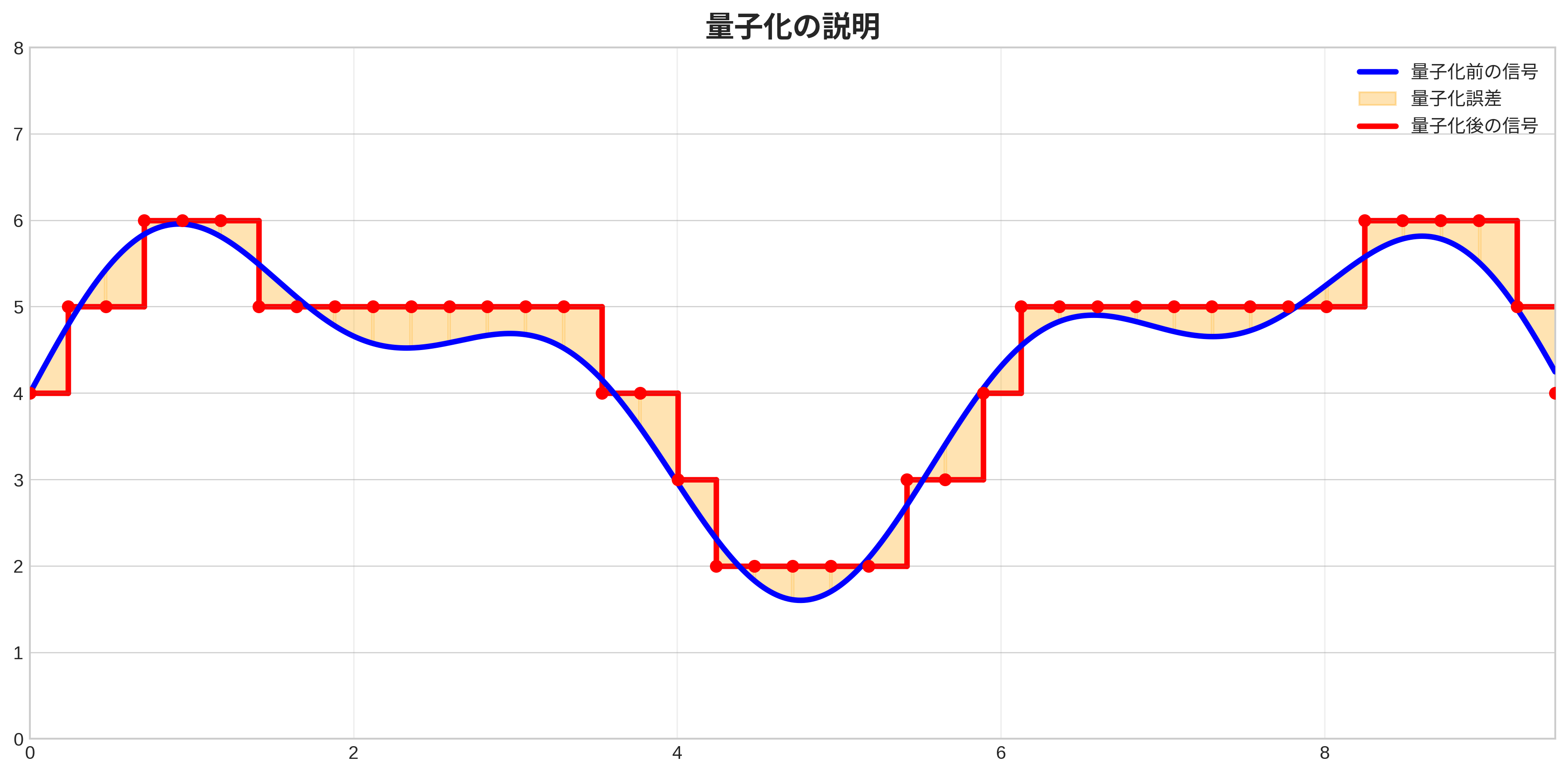量子化の概念図 量子化の概念図：青がfp32等の連続値とみなされる値、赤が量子化された値。この場合、x軸方向にもy軸方向にも量子化されている。

情報処理学会に寄稿した記事では、b1.58論文が報告したLLMの極小量子化によって精度が向上するという逆転現象について解説しました。この逆転現象は、通常であれば情報量を減らすと性能も下がるはずなのに逆に性能が向上したという、ある種、常識を覆す発見です。これまで、MNISTのような簡単なデータセットでは逆転現象の発生は確認されていましたが、LLMのような問題設定では発生が報告されたことはありませんでした。そのため、記事では「果たして、より大きな7Bモデルや30Bモデルでは、逆転現象は起きるのでしょうか。結果はまだ誰も知りません。これは面白くなってきました」と述べました。

あれから約1年が経過しましたが、この分野にはどのような進展があったのでしょうか。最新の研究を紹介していきましょう。なお、画像はすべて、紹介した論文からの引用です。

準備：そもそもなぜ量子化が重要なのか

近年のLLM（大規模言語モデル）はどれも、おおざっぱに分類するとAutoregressive（自己回帰型）なTransformer（トランスフォーマー）です。Autoregressiveというのは、あるstepでの出力を次のstepでの入力に使うという意味です。簡単に言えば、前の単語を使って次の単語を予測していく仕組みです。この仕組み上、LLMは以下のような問題を抱えています。

  • 1トークン（単語や文字の一部）を出力するたびに、毎回、モデルデータをDRAMからプロセッサに読み込む必要がある。通常、モデルは数GB～数十GBはあるので、1トークンを出力するために数十GBのデータを読み込む必要がある。
  • 1つの推論だけを処理する場合、学習時には行列積だった部分が行列-ベクトル積になるので、GPUの理論上の計算性能と実際に発揮できる性能が大幅に乖離する。
  • 複数の推論を同時に行う場合、kv-cache（過去の計算結果を保存しておくメモリ領域）のサイズが問題となるため、たくさんの推論処理は並列で実行できない（=理論性能と実効性能との乖離を埋めることがむずかしい）。

最近の高性能GPUは行列積の専用回路がのっているので、これを使いこなすことが大事になってくるわけですが、回路がたくさん搭載されすぎていて、行列積の回路にデータを供給しつづけるのも簡単なことではありません。モデルデータがちいさくなるのであれば、メモリ帯域を節約できるので、その分、行列積の回路にデータを供給しやすくなるわけです。それはすなわち、理論性能と実効性能との乖離を埋めることにつながります。

また、ちいさな端末（スマートフォンやエッジデバイスなど）で推論を行う場合には、そもそも、高性能なGPUに搭載されているHBM（High Bandwidth Memory、特殊で高速なメモリ）が使えません。そのため、DRAMの帯域がボトルネックになってしまう可能性が高くなります。このような場合にも、メモリ帯域が不足しがちなわけですから、モデルサイズが小さくなれば嬉しいわけです。

ちなみに、HBMはDRAMの一種で、GPUなどの演算チップのすぐ横にメモリチップを置くことでデータ転送速度（メモリ帯域）を稼ぎ、メモリそのものを積層することでメモリ容量を稼いでいます。HBMは高度な技術で製造されるため、チップの価格は同容量の普通のDRAMよりもはるかに高くなります。これが、高性能なGPUには高価なHBMが使われ、普及品には通常のDRAMが使われる理由です。

閑話休題、量子化によってデータのビット幅が下がるということは、演算器のビット幅も下げられるということです。LLMの演算ボトルネックである行列積（もしくは行列-ベクトル積）というのは積和算のかたまりですから、その専用回路の中には大量の乗算器が含まれています。乗算器は比較的大きな回路で、その大きさはおおざっぱには浮動小数点数の仮数部のビット幅の2乗になりますから、ビット幅が下がるというのは、演算器の回路面積も小さくできるということです。

要約すると、以下の2点が量子化のメリットとなります：

  • LLMのモデルは大きすぎるので、量子化によってモデルが小さくなると必要なメモリ帯域が小さくなるのでうれしい
  • ビット幅を下げると演算器が小さくなるので半導体の回路面積的にうれしい

論文紹介

論文1: EfficientQAT: Efficient Quantization-Aware Training for Large Language Models

Chenらは量子化を考慮した学習（Quantization-Aware Training）を効率的に行う手法を提案しました。b1.58論文ではweight行列に対して伝統的なStraight Through Estimatorを使って学習しているだけでしたが、EfficientQATでは、学習を二つのフェーズに分けて行うという工夫が入っています。第1フェーズではブロック単位で順次重みを量子化しながら全パラメータを学習し（block-wise training）、第2フェーズでは量子化オペレーターのスケーリングファクターとシフトファクターのみを学習します（end-to-end training）。これらの工夫により学習が大幅に効率化されるというのがEfficientQATの主張です。まず高精度（fp16やfp32）で学習済みのモデルがすでに存在し、それをさらに学習しながら量子化する、というのがこの手法の前提となっています。学習済みモデルのweightをいきなり全部量子化してしまう場合と比較してPerplexityが数十倍違う（Table 4、453.49 vs 7.68）という、劇的な結果になっています。

実験結果では、fp16モデルのweightを2、3、4ビットに量子化した場合、5つの常識推論タスクにおいて4ビットモデルはfp16とほぼ同等の精度、3ビットはやや低下、2ビットはさらに低い精度となりました。この結果はLlama 2の7B、3Bば70B、およびLlama 3の8Bと70Bモデルという広範なサイズで確認されています。

この研究ではb1.58論文のようにゼロからの量子化学習を行ったわけではないため、精度逆転現象を完全に否定する証拠とは言えませんが、逆転現象に対してどちらかというと否定的な結果と言えるでしょう。

論文2: BitNet a4.8: 4-bit Activations for 1-bit LLMs

Wangらは、BitNet b1.58の活性値（activation）を最小で4ビット幅にまで量子化するBitNet a4.8を提案しました（一部は8ビットのため、a4.8と呼ばれています）。特に興味深いのは、Llamaの700Mから7Bまでのモデルで実験が行われ、b1.58論文についての7Bモデルの結果が表（Table 1）に記載されている点です。

その結果を要約すると、小規模モデル（700M、1.3B）ではb1.58モデルはfpモデルより精度が低いものの、3Bではその差がわずか（fpモデル: 52.51、b1.58モデル: 52.30）となり、7Bでは逆転（fpモデル: 54.93、b1.58モデル: 55.09）しています。これはb1.58論文の結果とおおむね整合性があり、7Bモデルでも精度の逆転現象が発生したという結論を示しています。

この論文を発表したWangらはMicrosoft所属でb1.58論文と同じ研究グループなので、これは完全な追試とは言えませんが、大規模LLMの重みを三値に量子化すると精度が向上する可能性を示す有力な研究であると言えるでしょう。

論文3: BitNet v2: Native 4-bit Activations with Hadamard Transformation for 1-bit LLMs

Wangらは、b1.58 BitNetの活性値を4ビットに量子化するBitNet v2を提案しました。BitNet a4.8では一部（具体的には、MLPの2つ目のFC層）の層への入力が8bitになっていましたが、BitNet v2では全てのFC層への入力が4bitに量子化されます。

単純に8bitだったものを4bitにするだけでは精度が下がってしまいますから、ここで、一部の入力値の分布に外れ値が多い層については、アダマール変換を行うことで、情報量を落とさずに外れ値を減らし、正規分布に近い分布に変換することができます。アダマール変換でなぜ外れ値が減らせるのかは、ちょっと考えただけではわかりませんでした。

アダマール変換自体は、ナイーブに実装すると行列-ベクトル積になってしまいますが、フーリエ変換同様バタフライ演算で実装でき、この場合、入力ベクトルサイズ nn に対して nlog⁡(n)n \log(n)で実装できるのでオーダーがグッと下がるので問題なし、ということになっています。GPUで高速に実行できるのかはやや疑問でしたが、PyTorchから使えるCUDA実装が既に存在するようです。

さて、我々が知りたいのは論文の手法よりも、BitNet b1.58の大きなモデルについての実験結果です。実験の章では特に強調されていませんが、b1.58 BitNetの7Bモデルの結果が記載されており、BitNet a4.8論文よりも性能が向上しています。fp16モデルとの比較結果が記載されていないため、精度逆転現象については明確な主張は本論文からは得られませんでした。

論文4: Scaling Laws for Precision

Kumarらは、様々な設定でQuantization Aware Trainingをおこない、scaling lawを求めました。Fig. 4にはいくつかのサイズのモデルをweightのビット幅だけ変えつつ学習した結果が記載されていますが、ビット幅が下がるにつれてvalidation lossが上がっていくという、ある意味順当な結果となっています。

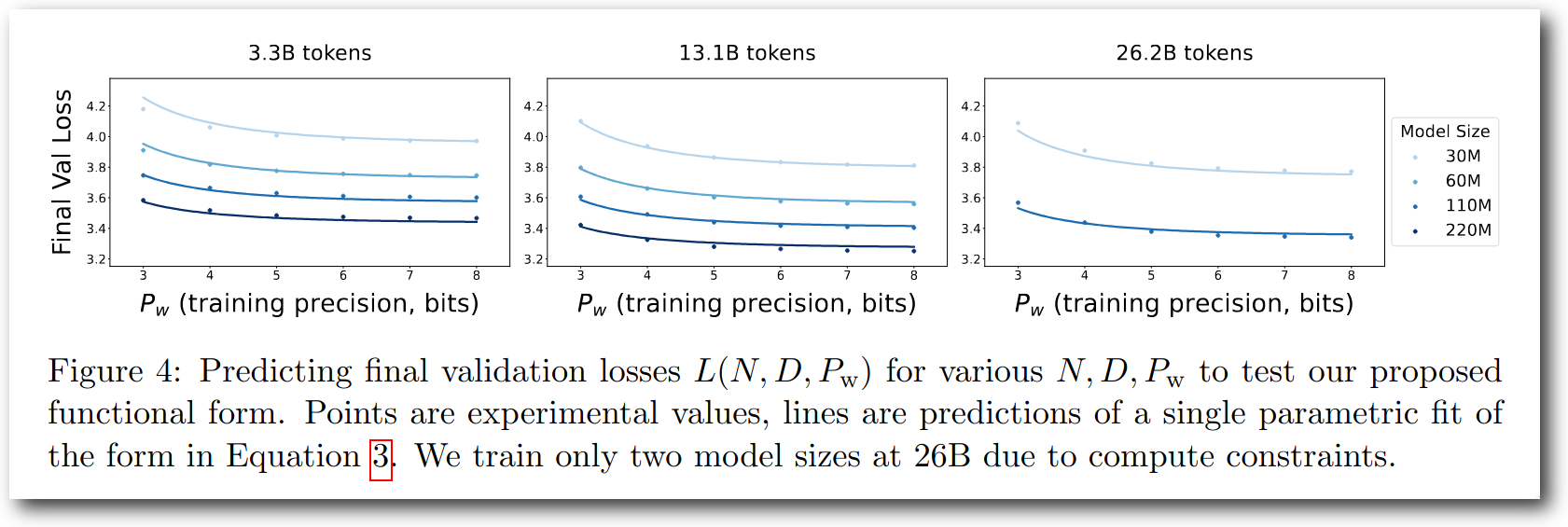Kumarらの論文のFigure 4 Figure 4: 様々なサイズのモデルをビット幅を変えて学習した結果。ビット幅が下がるにつれてvalidation lossが上昇している。

論文5: Scaling Law for Quantization-Aware Training

Chenらは、W4A4量子化についての様々な実験を行い、scaling lawを求めました。W4なので、今回着目しているb1.58とはちょっと違うのですが、興味深いことに、こちらの論文でも、MLPの2つ目のFC層は4bitに量子化すると性能が大きく劣化することが報告されています。

論文6: Compression Scaling Laws:Unifying Sparsity and Quantization

Frantarらは、Quantization Aware Trainingについて様々な設定で実験を行い、scaling lawを求めました。

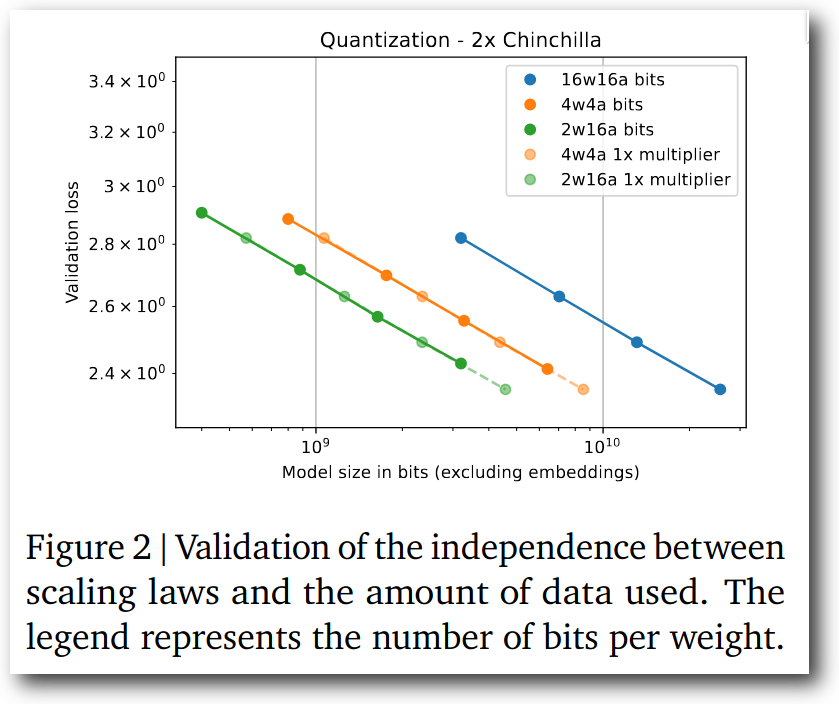Frantarらの論文のFigure 2 Figure 2: 量子化モデルと通常モデルのscaling lawの比較。

量子化前の16bitモデルと比較し、2bit weightモデルは、

  • モデルのファイルサイズが同等であれば、16bitモデルよりもかなりvalidation loss（perplexity）は下がる
  • モデルのパラメーター数が同等であれば、16bitモデルよりもvalidation lossは少し高くなる

という結果になっています。精度逆転現象に対しては否定的な結果です。図から読み取った限りでは、実験に使われたモデルは最も大きなもので1.5Bサイズなので、もう少し大きなモデルでの結果も見たいところではありますが、いずれにせよ、この直線を伸ばしていったところで、精度が逆転するようにはとても見えません。

論文7: QuEST: Stable Training of LLMs with 1-Bit Weights and Activations

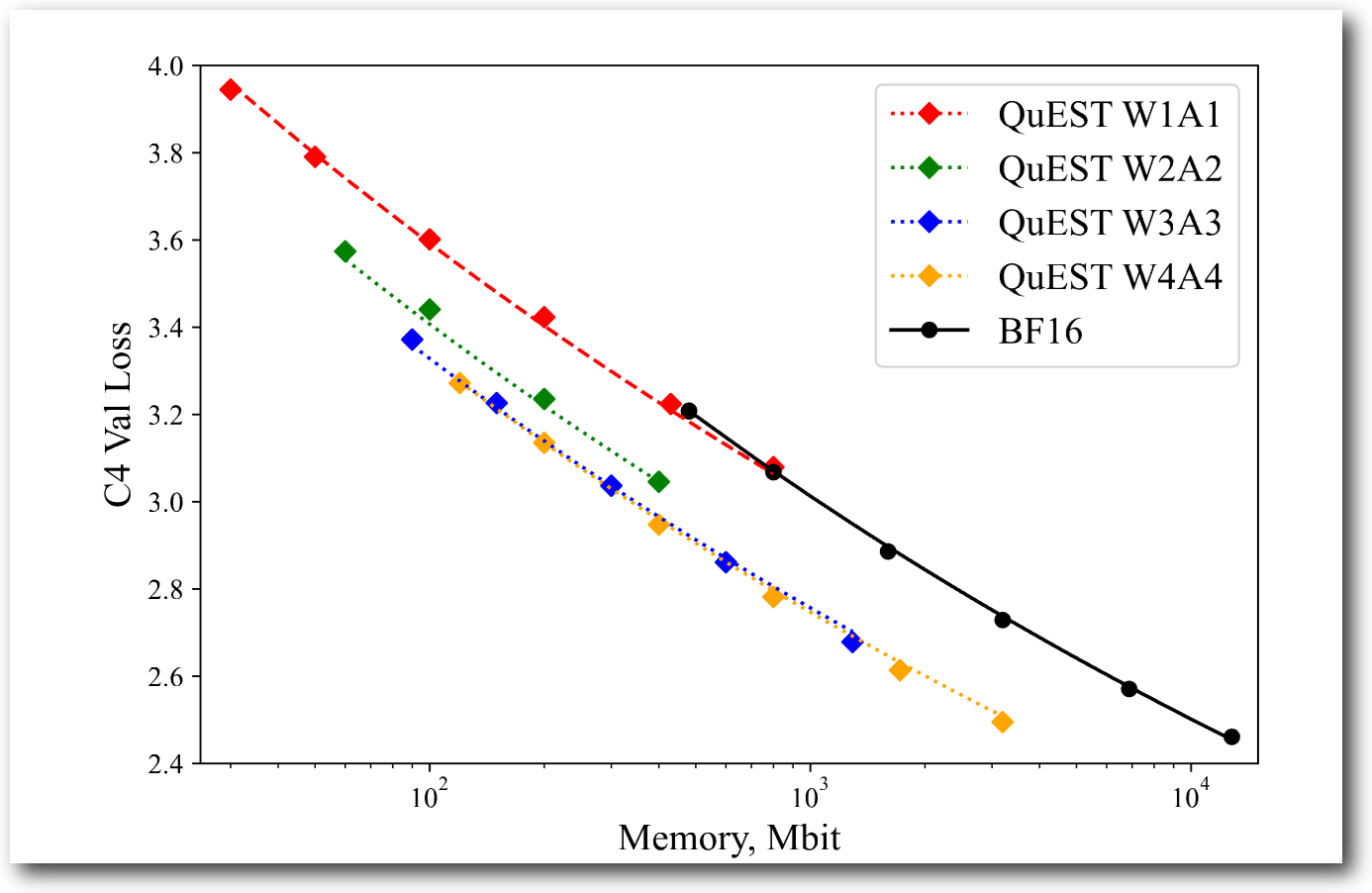
Panferovらは、量子化行列積の入力すべて（activationもweight matrixも）に前処理としてアダマール変換を適用することで、これまでよりも高性能な量子化ニューラルネットワークを得る方法を提案しました。BitNet v2と似ていますが、BitNet v2でのアダマール変換の適用が限定的であったのに対して、ほとんど全てのデータに対してアダマール変換を適用している点が違いと言えるでしょう。以下に引用した図1を見ると、bf16よりはw4a4の方が、モデルサイズだけを見るとメモリの利用効率が高い、という結果になっています。Franterらの実験結果とほぼ同様の結果ですね。

QuEST論文のFigure 1

まとめ

BitNet b1.58と同じグループからしか精度逆転現象の発生は報告されていません。しかも、そのグループから出ている最近の論文からは「精度が逆転するぞ」という主張は本文中にはありません。また、最近はQuantization Aware Trainingに関するscaling lawについての研究がいくつか出てきていますが、今回紹介した4本の論文のどれからも、モデルを大きくしたら1bit weightの方が精度が逆転しそうには読めません。どう結論付ければいいのか、正直、よくわからない状況です。

逆転現象は本来であれば学術的に非常に重要な発見であるはずで、実際、一度は世間からも大きな注目を集めたBitNetですが、その後続研究は2025年6月時点では世間から十分な注目を集めていません。英語圏も含め、7Bモデルでの精度逆転現象に言及した話題は今のところ見られません。また、BitNet a4.8やBitNet v2の論文でも、この逆転現象について特に強調されていません。不可解な点は多いものの、その重要性を考えると、結果の再現性についてはさらなる検証が必要と言えるでしょう。

もし精度の逆転現象が起こらないのだとすると、だから量子化はダメだ、という話になるわけではありませんが、最適なビット幅は何ビットなのかというのはかなり厄介な問題になります。最初の方に「乗算器の回路面積が減るのは嬉しい」と書きましたが、演算回数自体が増えるのだとすると、「乗算器の回路面積が減るのが嬉しいと見せかけて演算回数が増えるので乗算器の個数を増やしたら結局あんまり嬉しくなかった」という話になりかねないからです。実際にはさらにここに「演算回数が増えるので加算器の個数も増やさないといけないんだけど幅広な浮動小数点数数の加算器はめっちゃでかい」という問題もついてきます。つまり、モデルサイズだけを見て「weightのビット幅は1bitとか2bitがベストだね」と言えるのかというと、そんなに単純な話ではないんですね。

では実際のところは何ビットくらいがベストなのでしょうか。最後に私見を述べておきます。これまでのQuantization Aware Trainingについてのscaling lawに関する研究を見る限りは、量子化LLMのweightのビット幅はおそらく1〜6bitのどこかが最適なのだろうという点はおそらくこの分野をかじった人はほぼ全員が同意してくれると思います。これまでの経験上、1bitでは精度低下を補うためにパラメーター数を増やす必要があり、回路面積に対してはむしろ悪影響がでてしまう。2〜4bitのどれかを選択するとすると、3bitはソフトウェア側で扱いづらい、2bitと4bitだと、2bitの方に肩入れしたいが、おそらく主流となるのは4bitなのだろうなぁ、というのが現在の私の意見です。この予想を言い換えると、b1.58の時代はこない、もしくは、来るとしてもかなり遠い未来であるという主張になります。

さて、実際はどうなるでしょうか。5年後にこのエントリを見返して、予想が当たったかどうかを確認したいと思います。

さて、この長い長い記事を最後まで読んでいただいて、どうもありがとうございます。今回の記事はいかがでしたか？ この記事がお役に立ちましたら、XやFacebookでのシェアやXアカウントのフォローをいただけると幸いです。

お仕事募集中

PredNextでは現在、お仕事の依頼を募集しています。得意分野は自然言語処理や画像処理を中心とするAI関連技術ですが、ソフトウェア開発全般に対応可能です。もちろん、ニューラルネットワークの量子化も対象です。ご興味のある方はお問い合わせフォームからご連絡ください。

シェアする: