This article is a machine translation from Japanese. It may contain translation errors.

I’m Tokunaga, CEO of PredNext. On X and other platforms, I’m active with the ID tkng. For about the past 10 years, I’ve been passionate about neural network compression both professionally and personally, and in my previous position, as CTO of a company called LeapMind, I was involved in developing accelerators specifically for extremely quantized neural networks and neural network-specific accelerators specialized for fp8.

Because of that connection, about a year ago, I contributed an article to the Information Processing Society of Japan journal titled “Will the Era of 1-bit LLMs Come or Not, Which Is It?” (available for free in its entirety at the linked web version). The content explains the BitNet b1.58 paper (official title: “The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits,” research by Microsoft research team) that was a hot topic at the time. Note that the name “b1.58” means representing model parameters with ternary values (-1, 0, 1). When three types of values appear randomly and uniformly, entropy is about 1.58 bits, hence it’s called b1.58.

I’ve started with a barrage of technical terms, but what is quantization in the first place? Quantization is originally approximating continuous values with discrete values. However, in AI-related fields it’s a bit special: the operation of discretizing data to 8 bits or less, treating 32-bit floating-point numbers as continuous values, is called “quantization.” For example, while normal floating-point numbers are represented in 32 bits or 16 bits, reducing this to 8 bits, 4 bits, or even 1 bit can significantly reduce model size. Also, quantization to extremely small bit widths below 8 bits is called extremely low bit quantization or ultra low bit quantization, which we call “極小量子化” (extreme quantization) in Japanese.

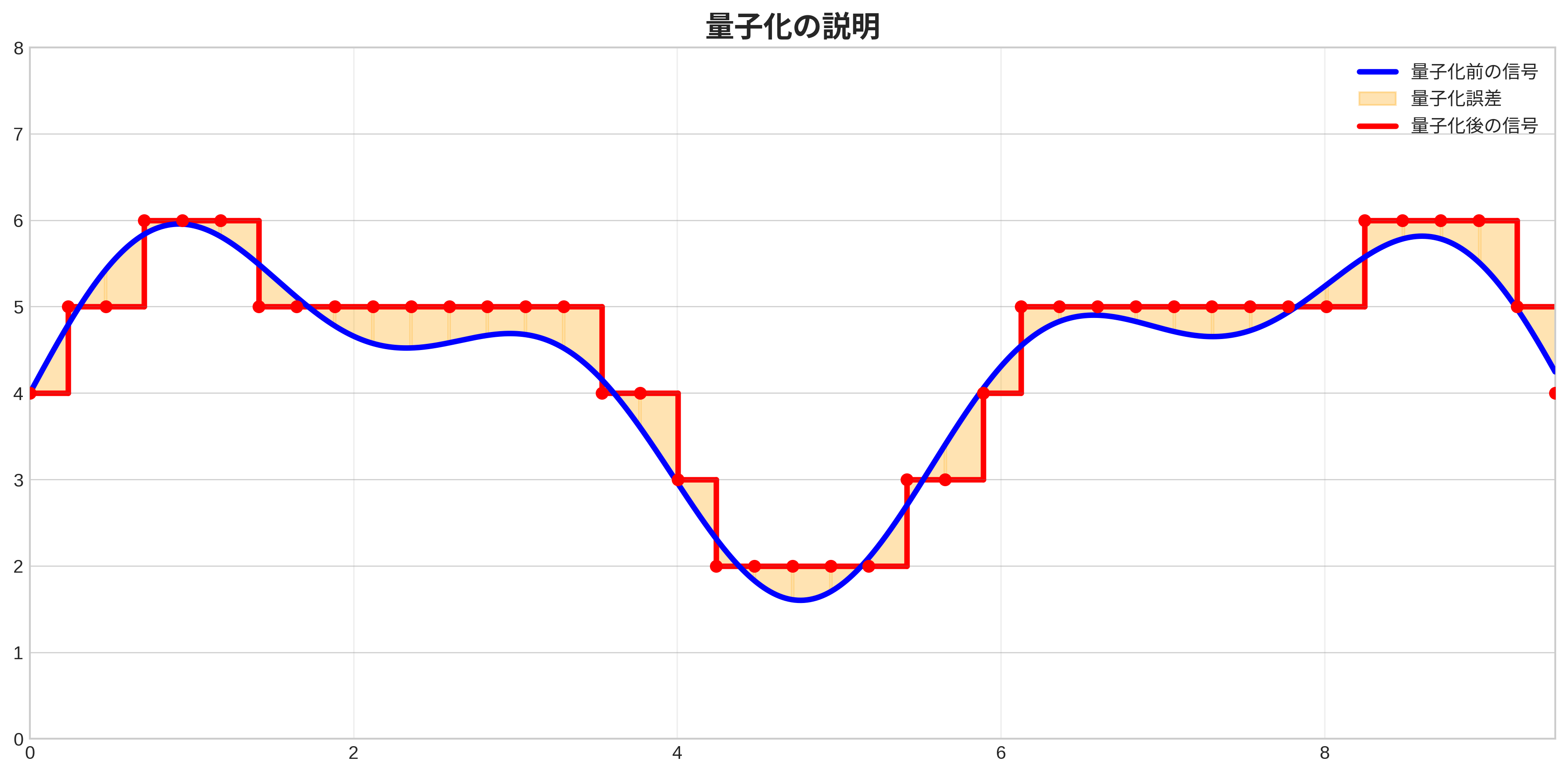Quantization concept diagram: Blue represents continuous values like fp32, red represents quantized values. In this case, quantization is performed in both x-axis and y-axis directions.

In the article I contributed to the Information Processing Society, I explained the reversal phenomenon where accuracy improves through extreme quantization of LLMs reported by the b1.58 paper. This reversal phenomenon is a discovery that in some sense overturns common sense: normally, performance should decrease when reducing information content, but instead performance improved. Previously, occurrence of the reversal phenomenon had been confirmed on simple datasets like MNIST, but had never been reported for problem settings like LLMs. Therefore, the article stated: “Will the reversal phenomenon occur in larger 7B or 30B models? No one knows the result yet. This is getting interesting.”

About a year has passed since then, but what progress has been made in this field? Let’s introduce the latest research. Note that all images are cited from the papers introduced.

Preparation: Why Is Quantization Important in the First Place?

Recent LLMs (Large Language Models) can roughly all be classified as autoregressive Transformers. Autoregressive means using the output of one step as input for the next step. Simply put, it’s a mechanism for predicting the next word using the previous word. Due to this mechanism, LLMs have the following problems:

• Every time one token (part of a word or character) is output, model data must be loaded from DRAM to the processor. Since models are usually several GB to several tens of GB, tens of GB of data must be loaded to output one token.
• When processing only one inference, parts that were matrix multiplications during training become matrix-vector multiplications, causing a large gap between GPU theoretical computational performance and actually achievable performance.
• When performing multiple inferences simultaneously, the size of kv-cache (memory area storing past calculation results) becomes an issue, so many inference processes cannot be executed in parallel (= difficult to close the gap between theoretical and effective performance).

Recent high-performance GPUs have dedicated circuits for matrix multiplication, so making full use of these becomes important, but too many circuits are installed, and continuously supplying data to the matrix multiplication circuits isn’t simple either. If model data becomes smaller, memory bandwidth can be saved, making it easier to supply data to matrix multiplication circuits. That is, it leads to closing the gap between theoretical and effective performance.

Also, when performing inference on small terminals (smartphones, edge devices, etc.), HBM (High Bandwidth Memory, special high-speed memory) installed on high-performance GPUs cannot be used in the first place. Therefore, there’s a high possibility that DRAM bandwidth becomes the bottleneck. In such cases too, since memory bandwidth tends to be insufficient, smaller model sizes would be welcome.

Incidentally, HBM is a type of DRAM that achieves data transfer speed (memory bandwidth) by placing memory chips right next to computational chips like GPUs, and achieves memory capacity by stacking the memory itself. Since HBM is manufactured with advanced technology, chip prices are far higher than ordinary DRAM of the same capacity. This is why expensive HBM is used in high-performance GPUs, while ordinary DRAM is used in popular products.

Back to the topic, lowering data bit width through quantization means the bit width of arithmetic units can also be lowered. Matrix multiplication (or matrix-vector multiplication), which is the computational bottleneck of LLMs, is a mass of multiply-accumulate operations, so dedicated circuits for this contain a large number of multipliers. Multipliers are relatively large circuits, and their size is roughly the square of the mantissa bit width of floating-point numbers, so lowering bit width means circuit area of arithmetic units can also be reduced.

In summary, the following two points are the merits of quantization:

• LLM models are too large, so when models become smaller through quantization, required memory bandwidth decreases, which is welcome
• Lowering bit width makes arithmetic units smaller, which is welcome in terms of semiconductor circuit area

Paper Introductions

Paper 1: EfficientQAT: Efficient Quantization-Aware Training for Large Language Models

Chen et al. proposed a method for efficiently performing Quantization-Aware Training. While the b1.58 paper only used the traditional Straight Through Estimator for weight matrices during training, EfficientQAT incorporates the innovation of dividing training into two phases. In the first phase, all parameters are trained while sequentially quantizing weights block by block (block-wise training), and in the second phase, only the scaling factors and shift factors of quantization operators are trained (end-to-end training). The claim of EfficientQAT is that these innovations significantly improve training efficiency. The premise of this method is that a model already trained at high precision (fp16 or fp32) exists, which is then further trained while being quantized. Compared to the case of immediately quantizing all weights of a trained model, the Perplexity difference is dramatic (Table 4, 453.49 vs 7.68).

In experimental results, when fp16 model weights were quantized to 2, 3, and 4 bits, 4-bit models achieved almost the same accuracy as fp16 on five commonsense reasoning tasks, 3-bit showed slight degradation, and 2-bit showed even lower accuracy. These results were confirmed across a wide range of sizes: Llama 2’s 7B, 3B and 70B, and Llama 3’s 8B and 70B models.

Since this research didn’t perform quantization training from scratch like the b1.58 paper, it can’t be said to be evidence completely denying the accuracy reversal phenomenon, but it can be said to be a somewhat negative result regarding the reversal phenomenon.

Paper 2: BitNet a4.8: 4-bit Activations for 1-bit LLMs

Wang et al. proposed BitNet a4.8, which quantizes BitNet b1.58’s activations to a minimum of 4-bit width (some are 8-bit, hence called a4.8). Particularly interesting is that experiments were conducted on Llama models from 700M to 7B, and results for 7B models regarding the b1.58 paper are listed in a table (Table 1).

Summarizing those results, while b1.58 models have lower accuracy than fp models for small models (700M, 1.3B), at 3B the difference becomes slight (fp model: 52.51, b1.58 model: 52.30), and at 7B it reverses (fp model: 54.93, b1.58 model: 55.09). This is roughly consistent with the results of the b1.58 paper, showing the conclusion that the accuracy reversal phenomenon occurred even with 7B models.

Since Wang et al. who published this paper are from Microsoft and the same research group as the b1.58 paper, this can’t be called a complete replication, but it can be said to be powerful research showing the possibility that quantizing large LLM weights to ternary values improves accuracy.

Paper 3: BitNet v2: Native 4-bit Activations with Hadamard Transformation for 1-bit LLMs

Wang et al. proposed BitNet v2, which quantizes b1.58 BitNet’s activations to 4 bits. While in BitNet a4.8 inputs to some layers (specifically, the second FC layer of MLP) were 8-bit, in BitNet v2 all FC layer inputs are quantized to 4-bit.

Simply changing from 8-bit to 4-bit would degrade accuracy, so here, for layers with many outliers in the distribution of some input values, Hadamard transformation is performed to reduce outliers and transform to a distribution close to normal distribution without losing information content. I couldn’t immediately understand why Hadamard transformation can reduce outliers.

Hadamard transformation itself becomes matrix-vector multiplication if naively implemented, but like Fourier transformation can be implemented with butterfly operations, in this case it can be implemented in $n \log(n)$ for input vector size $n$, so the order drops significantly and there’s no problem. There was some doubt whether it can be executed fast on GPU, but a CUDA implementation usable from PyTorch already exists.

Now, what we want to know more than the paper’s methodology is experimental results on larger models of BitNet b1.58. While not particularly emphasized in the experimental chapter, results for 7B models of b1.58 BitNet are listed, and performance has improved over the BitNet a4.8 paper. Since comparison results with fp16 models aren’t listed, clear claims about the accuracy reversal phenomenon couldn’t be obtained from this paper.

Paper 4: Scaling Laws for Precision

Kumar et al. performed Quantization Aware Training in various settings and obtained scaling laws. Fig. 4 shows results of training models of several sizes while changing only weight bit width, and validation loss increases as bit width decreases—a reasonable result in some sense.

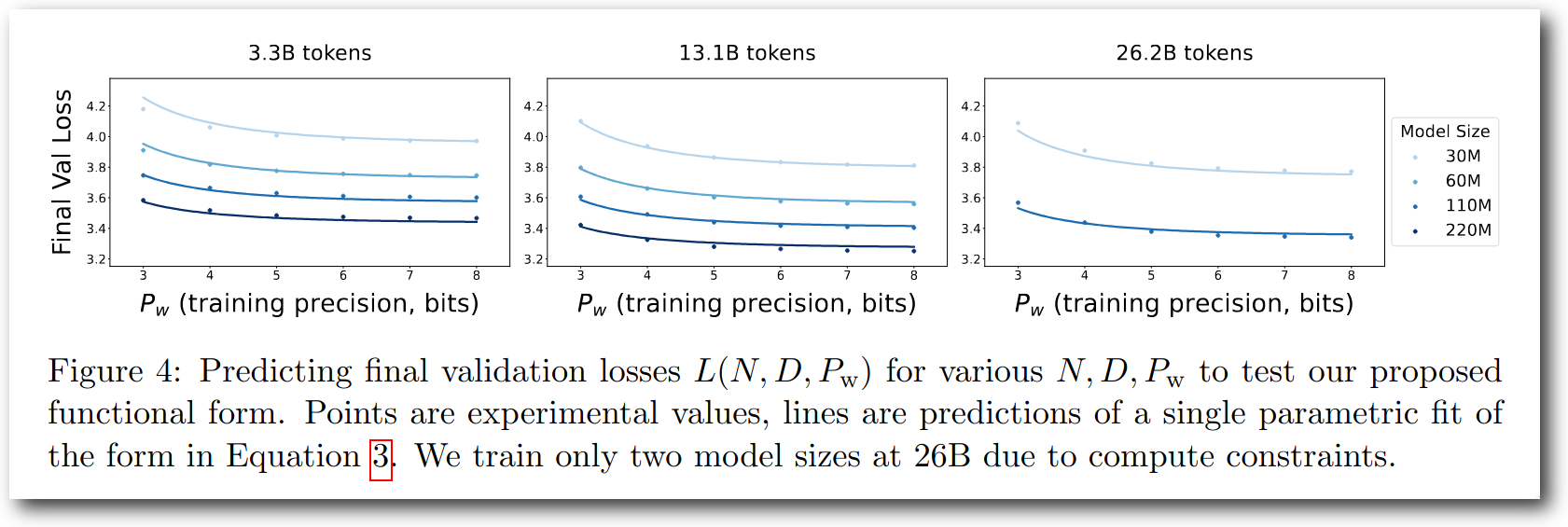Figure 4: Results of training models of various sizes with different bit widths. Validation loss increases as bit width decreases.

Paper 5: Scaling Law for Quantization-Aware Training

Chen et al. conducted various experiments on W4A4 quantization and obtained scaling laws. Since it’s W4, it’s a bit different from the b1.58 we’re focusing on, but interestingly, this paper also reports that performance significantly degrades when the second FC layer of MLP is quantized to 4 bits.

Paper 6: Compression Scaling Laws: Unifying Sparsity and Quantization

Frantar et al. conducted experiments in various settings on Quantization Aware Training and obtained scaling laws.

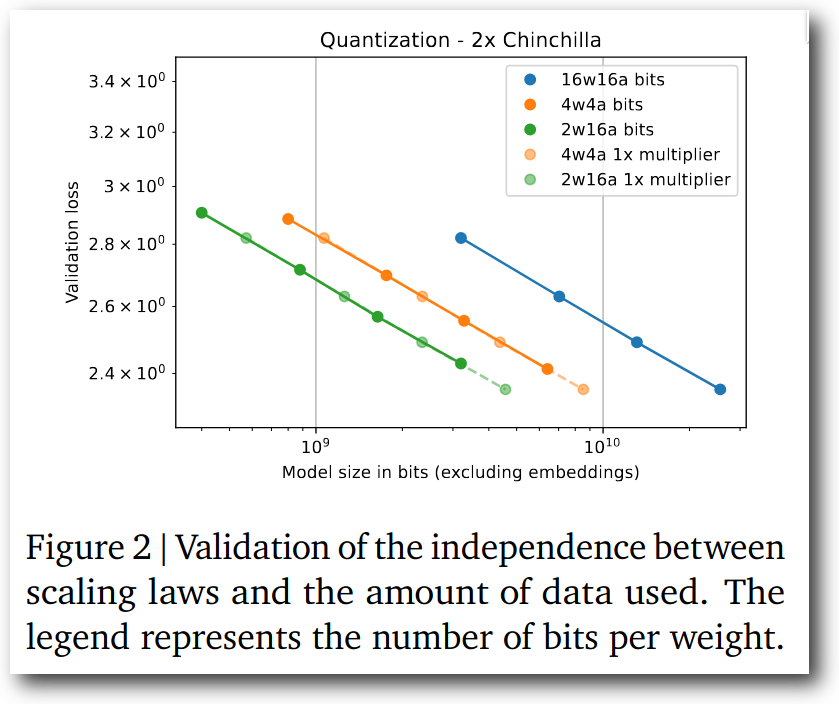Figure 2: Comparison of scaling laws for quantized and normal models.

Compared to pre-quantization 16-bit models, 2-bit weight models:

• If model file size is equivalent, validation loss (perplexity) is considerably lower than 16-bit models
• If model parameter count is equivalent, validation loss is slightly higher than 16-bit models

This result argues against the accuracy reversal phenomenon. As far as I could read from the figure, the largest model used in experiments was 1.5B size, so I’d like to see results from slightly larger models, but in any case, extending this line doesn’t seem likely to result in accuracy reversal.

Paper 7: QuEST: Stable Training of LLMs with 1-Bit Weights and Activations

Panferov et al. proposed a method to obtain higher-performance quantized neural networks than before by applying Hadamard transformation as preprocessing to all inputs of quantized matrix multiplication (both activation and weight matrix). While similar to BitNet v2, the difference is that Hadamard transformation is applied to almost all data, whereas in BitNet v2 application of Hadamard transformation was limited. Looking at the cited Figure 1 below, in terms of memory utilization efficiency when looking only at model size, w4a4 is higher than bf16. This is almost the same result as Frantar et al.’s experimental results.

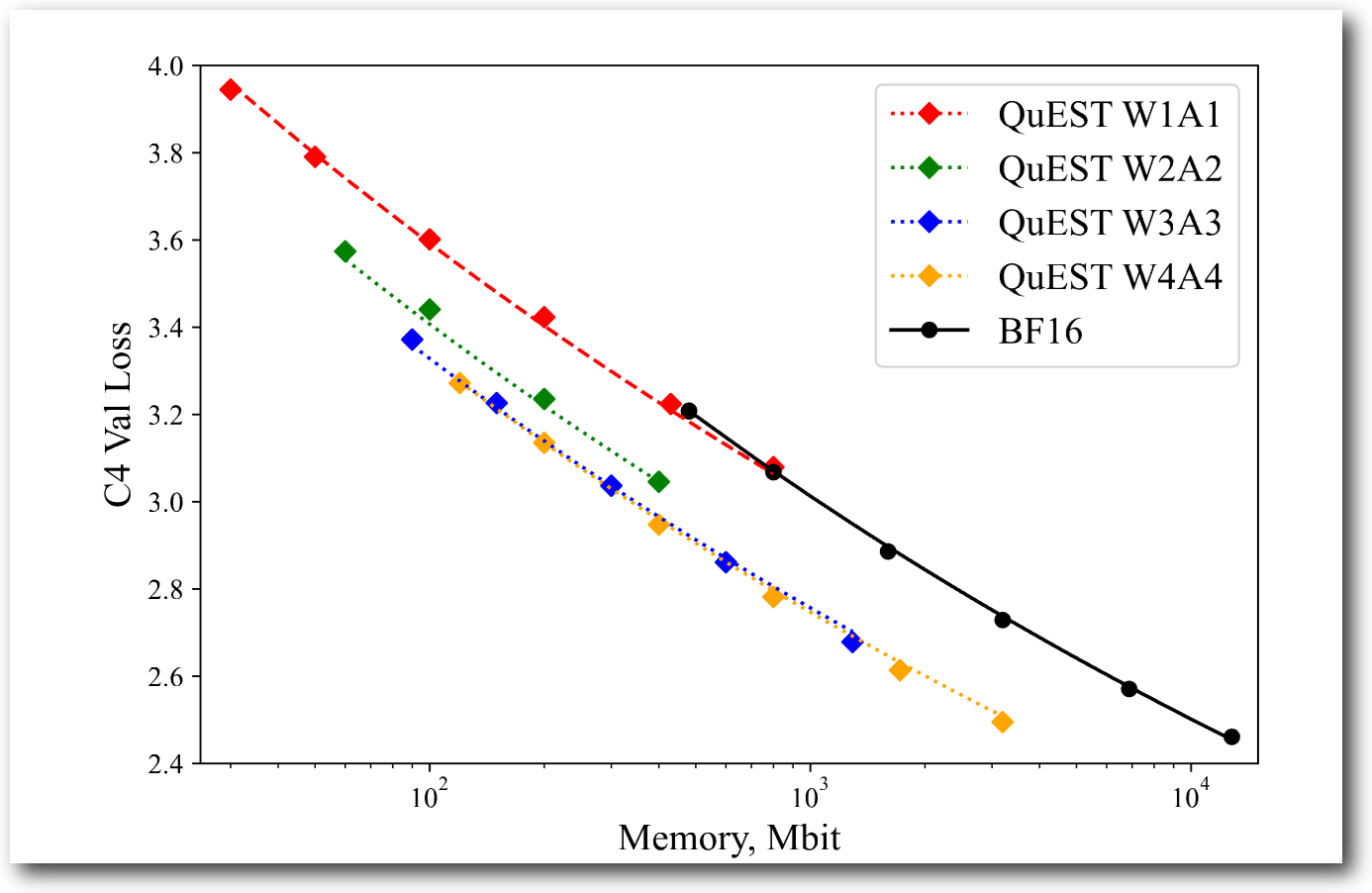
Summary

Occurrence of the accuracy reversal phenomenon has only been reported from the same group as BitNet b1.58. Moreover, recent papers from that group don’t have claims in the main text saying “accuracy will reverse.” Also, several studies on scaling laws regarding Quantization Aware Training have emerged recently, but from any of the four papers introduced this time, it doesn’t seem like 1-bit weight accuracy will reverse if models are made larger. Honestly, it’s hard to draw a clear conclusion at this point.

The reversal phenomenon should originally be a very important academic discovery, and BitNet actually drew great attention from society once, but subsequent research as of June 2025 isn’t receiving sufficient attention from society. Including English-speaking areas, no topics mentioning the accuracy reversal phenomenon with 7B models have been seen so far. Also, even in the BitNet a4.8 and BitNet v2 papers, this reversal phenomenon isn’t particularly emphasized. While there are many puzzling points, considering its importance, further verification of result reproducibility is necessary.

If the accuracy reversal phenomenon doesn’t occur, it doesn’t mean quantization is bad, but the question of what bit width is optimal becomes quite tricky. I wrote earlier that “reducing multiplier circuit area is welcome,” but if the number of operations itself increases, it could become a story of “it seemed welcome that multiplier circuit area decreased, but since operation count increases, if we increase the number of multipliers, it wasn’t actually that welcome after all.” In practice, there’s also the problem that “since operation count increases, we need to increase the number of adders, but wide floating-point number adders are huge.” In other words, looking only at model size and saying “1 bit or 2 bits is best for weight bit width” isn’t such a simple story.

So what bit width is actually best for weights? Let me state my personal opinion at the end. Looking at research on scaling laws for Quantization Aware Training so far, I think almost everyone who’s touched this field would agree that the optimal bit width for quantized LLM weights is probably somewhere between 1-6 bits. From past experience, at 1 bit, parameter count needs to be increased to compensate for accuracy degradation, and to secure the same speed while increasing parameter count, adders (large!) need to be increased, which would actually negatively affect circuit area. So 1 bit is probably not good. My personal feeling is that around 4 bits would probably work, and then it becomes a question of which is best among 2-4 bits, and 3 bits is difficult to handle on the software side. Between 2 bits and 4 bits, I’d lean toward 2 bits, but it seems like a quite risky choice, so what becomes mainstream will probably be 4 bits—that’s my current opinion.

Rephrasing this prediction, the era of b1.58 won’t come, or if it does, it will be in the distant future. Now, what will actually happen? I’d like to look back at this entry in 5 years and check if the prediction was correct.

Thank you very much for reading this long article to the end. How was this article? If you found this article helpful, I’d appreciate it if you could share it on X or Facebook or follow our X account.

Looking for Work

PredNext is currently accepting project requests. Our specialty is AI-related technologies centered on natural language processing and image processing, but we can handle software development in general. Of course, neural network quantization is also covered. If you’re interested, please contact us through our contact form.